
Year 13 Revision Day Calculus.
Friday 26th April 2019
University of Hertfordshire, Hatfield.
I was privileged, as an AMSP associate, to be asked by Val Pritchard, area coordinator for Hertfordshire, to assist her in presenting the first full revision day for the new specification A level. Having spent two years working with students across three boards, OCR, OCR (MEI) & Edexcel I was delighted to accept. I had a good idea that it would be well attended and indeed there were 72 students from 10 local schools.
Whilst the accompanying teachers attended their own sessions with Joanna Deko and Natalie Vernon, the students began at 9.15am with a gentle warm up, from Val, on simplifying algebra and a discussion on any possible misconceptions. For example
seamlessly picked up again in the first session, on preparing algebra for differentiation and integration when students were given
and a suggested preparation on mini white boards was given as
I hadn’t seen that one coming, it was as if she had planned it! The correct preparation being
Algebra preparation led into my first presentation on how to speed up on differentiation and integration, time pressure being a crucial factor in the new spec. It was lovely to be able to show them how to differentiate and integrate using ‘inspection’ rather than using a substitution ‘u’. There is rarely time to do this formally in school.

Students were given plenty of practice, 20 questions and I was pleased to be able to speed up my feedback by using a QR code for answers. Did you know it will work from the back of a lecture theatre?!

(Apologies to those who did not have the QR code app).
Reminder: Learn to differentiate 2x, it’s in the syllabus and hence the integration.
The second session on differentiation from first principles seemed another gentle build up to the problem solving exam questions to come. However, Val highlighted the trickier questions on trig which may require students to use the small angle approximations in their differentiation and the questions requiring the gradient at a point. I have seen students confident with differentiation from first principles wobble with a question like
f(x) = 3x2 – 2x +3
a) Find f(4 + h)
b) Hence, using differentiation from first principles find f ‘(4)
My advice, practise these questions.
Session three on the Newton Raphson formula began with some lovely GeoGebra visuals on how the formula works and when it will fail, f‘(x) = 0 . Four multiple choice questions and then it was quickly into the problem solving exam questions covering all the morning’s work. Reinforcements were sent for and the accompanying teachers returned to help with this part. Some really challenging questions here without the step by step guidance seen in the old spec. My highlights here were i) a student asking if u = ex would work on
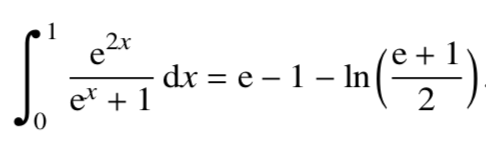
A question taken from OCR C4 June 2006 Q6ii but with the steps taken out (harsh! but by all means possible in the spirit of the new spec). The step given in the original paper was to use u = ex + 1. Having prepped in advanced I took this as THE substitution but u=ex works quite well too.
ii) The 18 marker from AQA C2 Jan 2006 Q8, with the steps taken out again! A lovely question on geometry, differentiation and integration all in one question. I think I will remember this one.
Time for a well-earned lunch and some fresh air before the afternoon start. A great buffet and time to catch up with colleagues.
As the students returned for the afternoon, they definitely needed some encouragement as they began their fourth hour of Maths so I passed on a message from Corbett Maths

Thank you Mr Corbett, it was much appreciated and gave us a boost to start the fourth session, Calculus and Kinematics. My turn again, I started the students off with the basic theory and a couple of questions on 1D kinematics; one example & one for them. Moving on to 2D, I had already experienced some unfamiliarity here with my own students. I reminded students to put in a constant of integration for both the i and the j vector when necessary. The newness of this topic hit me when I stumbled over what to call the value in front of either vector, is it ‘the coefficient of i’, ‘the magnitude of i’, ‘the value of i’? I plumped for ‘the coefficient of i’, answers on a postcard please. A reminder too, to draw a diagram, simple but so effective (possibly not much time to draw elaborate pictures of ships).
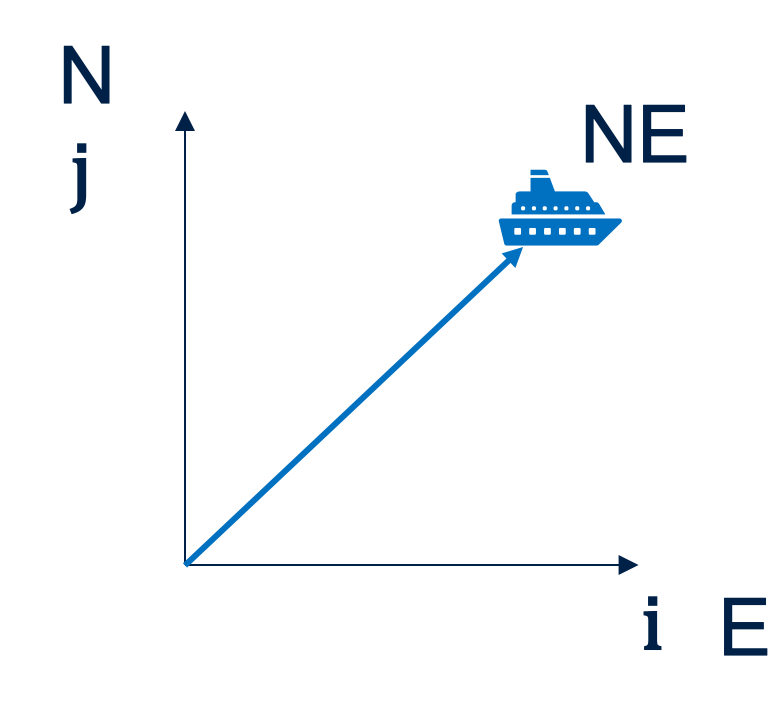
It was with great delight that I read the feedback from one student that they had learnt to connect the compass directions, North and East with the i and j vectors respectively
Some more lovely feedback
The fifth session on differential equations provided the students with a reminder of the difference between a general solution (referred to as a family👨👩👧👦 of functions) and a particular solution (one member of the family👩). A couple of questions to reinforce the topic and then a second session on problem solving exam questions. Some more fantastic questions selected by Val. Well done to Robert & Beth for keeping me focussed on a challenging rabbit population and height of the waves question respectively, in the fifth hour of the day🤪 Thank you Ben for rescuing me with your answers. Pretty impressed with Michael and his neighbour too for sticking with it. That said, all the students worked amazingly hard, very well done. You all deserve to do well in your exams on the 5th, 12th and 14th June, Good Luck.
Thank you to Val, Jo, Natalie, Kathy, the teachers and the students for making it such a rewarding day. Will I do it again? Give me a year to move on, I might forget the fear of standing up in front of 70 plus students and the hard work and say Yes😂
Picture of Val Pritchard at the end of the day, looking as if she could do another five hours!

Top Tips:
1. Use the sample papers from all the exam boards and time yourself.
2. Use the formula sheet.
3. Know your calculator.
Best Bit: seeing the fruits of my labour from four years ago in a student who I had taught in Year 9, now thriving doing A level Maths in Year 13. I hadn’t seen him for four years.
If there are any errors, omissions or misrepresentations please email [email protected]

I have an offer of ‘the j component’.
Wonderful to read about the positive work you are doing with so many enthusiastic students! Thanks for sharing this.